Simplify Your Integral Calculus with Bảng Nguyên Hàm – The Ultimate Time-Saving Tool

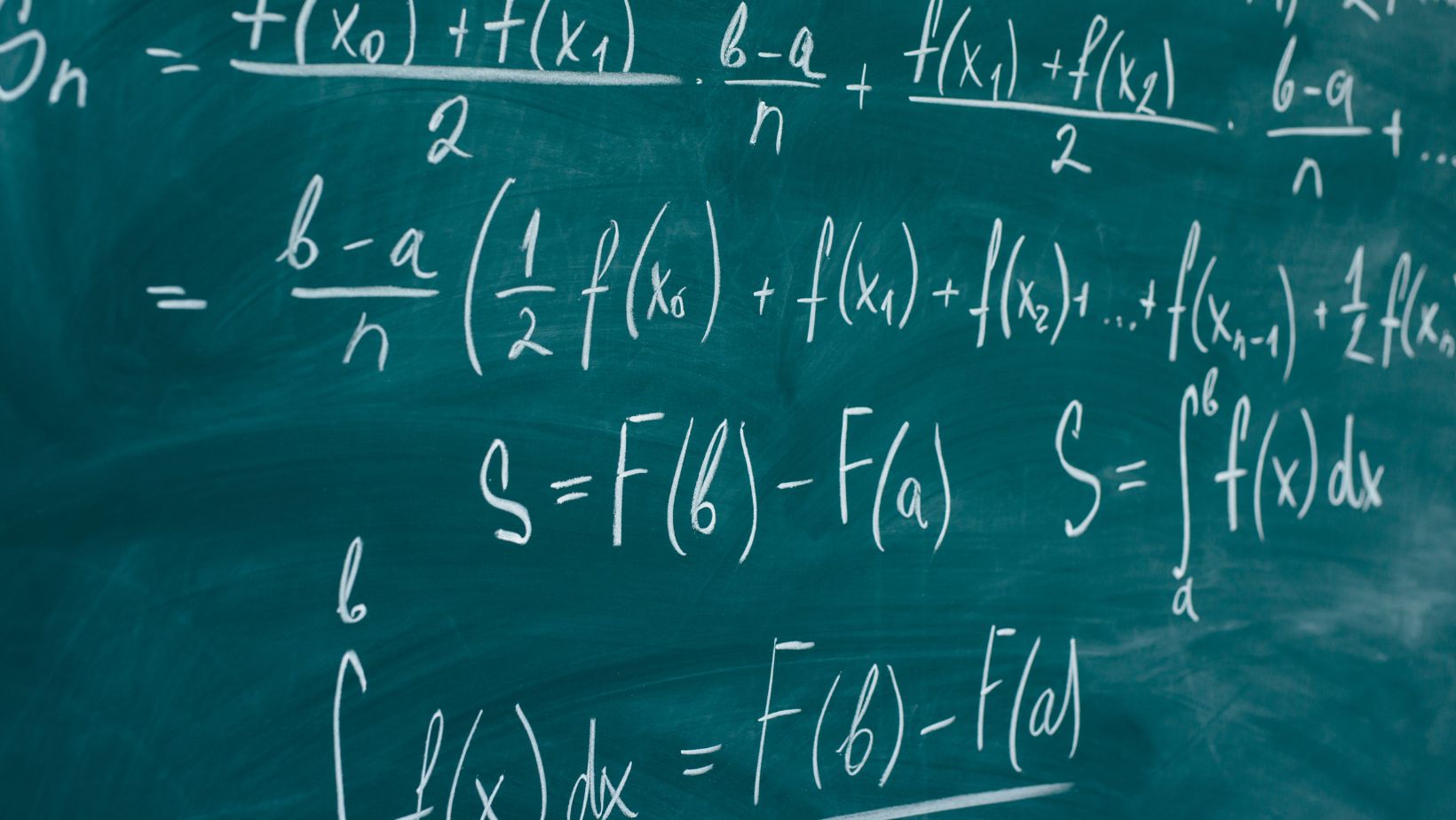
Have you ever heard of “bảng nguyên hàm”? If you’re interested in mathematics and calculus, then you’re in for a treat. In this article, I’ll be diving into the fascinating world of “bảng nguyên hàm” and exploring its importance in calculus.

So, what exactly is “bảng nguyên hàm”? Well, it’s a concept that plays a crucial role in calculus, particularly when it comes to finding derivatives. Essentially, “bảng nguyên hàm” is a table that lists the derivatives of common functions. It provides a quick and convenient way to find the derivative of a function without having to go through the complex process of differentiation.

Bảng Nguyên Hàm

Definition of Derivative

A derivative is a fundamental concept in calculus that represents the rate at which a function is changing. It measures the sensitivity of the function to infinitesimally small changes in its inputs. In simpler terms, it tells us how the function is behaving at any given point.

Geometric Interpretation of Derivative

The derivative of a function can also be interpreted geometrically. It represents the slope of the tangent line to the curve of the function at a specific point. This slope indicates the steepness or the rate of change of the function at that point.

Thinking about it visually, imagine a roller coaster track. The slope of the track at any point tells us how steep the drop or climb is at that particular moment. Similarly, the derivative of a function gives us information about the steepness or the rate of change of the function at a specific point.

Physical Interpretation of Derivative

In addition to its geometric interpretation, the derivative can also have physical meaning. In physics, the derivative represents the rate of change of a physical quantity with respect to another quantity. For example, the derivative of position with respect to time gives us the velocity of an object.

By calculating derivatives, we can analyze how quantities such as distance, velocity, acceleration, and more, change over time. This physical interpretation helps us understand and model various real-world phenomena.

Understanding derivatives is crucial in calculus as they are the building blocks for more advanced concepts like integration and optimization. They play a vital role in describing and analyzing the behavior of functions in mathematics and their applications in the real world.

In the next section, let’s delve into the concept of “bảng nguyên hàm” and explore how it simplifies the process of finding derivatives.

What is an Integral?

Definition of Integral

An integral is a fundamental concept in calculus that represents the cumulative sum of a function over a given interval. It is the reverse process of finding derivatives, and it allows us to determine the total accumulation of a quantity.

In mathematical terms, the integral of a function f(x) is denoted by the symbol ∫f(x)dx, where dx represents an infinitesimally small change in the independent variable x. The integral is computed by finding the antiderivative, or the function whose derivative is equal to the integrand.

Geometric Interpretation of Integral

Geometrically, the integral can be visualized as the area under a curve. By calculating the definite integral, we can determine the exact area between the function and the x-axis within a specified interval.

The concept can be illustrated by considering a simple example of finding the integral of a non-negative function. Suppose we have a function f(x) = x^2, and we want to find the area under the curve between x = 1 and x = 3. By evaluating the definite integral ∫[1,3]x^2 dx, we can determine the precise area bounded by the curve, the x-axis, and the vertical lines x = 1 and x = 3.

Physical Interpretation of Integral

In addition to its geometric interpretation, the integral also has a physical significance. It can represent quantities such as displacement, velocity, and acceleration in physical systems.

For instance, if we consider a particle moving along a straight line, the integral of its velocity function with respect to time gives us the particle’s displacement. Similarly, integrating the acceleration function with respect to time yields the particle’s velocity.

By utilizing the concept of integrals, we can analyze and calculate various physical properties and quantities related to motion, such as finding the distance traveled by an object and determining the change in speed over a given time interval.

Understanding the concept of integrals is essential in calculus as it allows us to solve a wide range of problems related to areas, accumulations, and physical quantities. Next, let’s explore more about the practical applications and benefits of “bảng nguyên hàm” in simplifying the process of finding integrals.