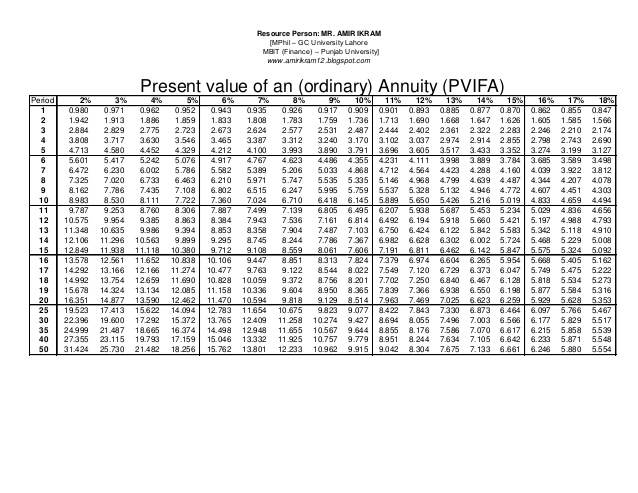
Present Value of $1 Annuity Table

Most people have trouble understanding how an annuity works, even though it is quite simple conceptually. This is because they try to think of the future as a lump sum of money instead of as a series of future payments, and get confused by the fact that a future payment of $1000 is “worth” a much higher amount than a future payment of $1000.

The blog is a financial blog, which means that it is about Finance or financial issues. It is not a finance blog about re-engineering or finance. The blog may also have other subjects like finance, finance analysis, finance blogs, finance blogs for beginners, finance blogs for children, etc.

The present value is the value in present terms of the amount a series of future cash flows are expected to be worth. The present value is equal to the sum of the present values of the cash flows. The present value of a series of future cash flows is the amount expected to be received at the end of the period multiplied by the sum of the interest rate and the number of cash flows.

Accounting Home Table of present value of annuity in $1.

18. September 2020
Accounting Adam Hill

However, there are an infinite number of periods for perpetual bonds, so we need a formula to find the PV. The formula for calculating PV is the amount of each payment divided by the interest rate. PV for annuities – Temporary and periodic annuities can be calculated based on benefit amount, interest rate and number of periods. With a periodic annuity, on the other hand, the payments are made at the end of the period. This means that the first payment is made one period after the annuity has started and that the last payment is made at the very end.

Another way to look at it is to see how much the annuity owed will be worth when the payments are completed in the future, advanced to the present. The initial payment bears interest at a periodic rate (r) over several payment periods (n). PVIFA is also used in the formula for calculating the present value of the annuity.

A payable annuity exists if each payment is due at the beginning of the period; a current annuity exists if the payment is due at the end of the period. A common example of an annuity is rent that is due at the beginning of the lease term. The present value annuity calculator is used to calculate the present value of a periodic annuity, which is the present value of a stream of equal payments made at regular intervals over a period of time.

The risk is adjusted according to the duration of the annuity payments and the investment instrument used. Higher interest rates result in lower net present value calculations.

Calculate the percentage present value annuity factor (PVIFA) and create a table of PVIFA values. Construct a compound interest table for the present value of a regular annuity or the present value of an annuity with payments of $1. The present value percentage of an annuity is helpful in deciding whether to pay principal now or choose to pay an annuity in future periods. Using the estimated returns, you can compare the cost of annuities to the cost of capital. The present value factor can only be calculated if annuity payments are made for a predetermined amount during a predetermined period.

There are different JV calculations for annuities and regular annuities, depending on the date of the first and last payment. Annuities may be valued by calculating the actuarial present value of future contingent annuity payments.

Using the amount of the payment, the number of payments and the rate of return, the cost of today’s payments in dollars is calculated. They can occur in loans, retirement plans, leasing, insurance plans, tax plans, etc.

This is because the value of a dollar is falling today while high returns are expected in the future. There are certain formulas that make it easier to calculate the AVF of an annuity. The present value of annuity payable (PVP) is a calculation of the value at the end of a specified number of periods using the present value of money.

It is sometimes interesting to see how the flow of recurring payments increases after a few periods. An annuity is an annuity with benefits at the beginning of each period; a periodic annuity is an annuity with benefits at the end of the period. The present value of an annuity, sometimes called an immediate annuity, is used to calculate a series of periodic payments or cash flows that begin immediately. An annuity is a series of payments made at regular intervals and in equal amounts over time.

The fact that the value of the annuity to be paid is greater is logical because all payments are pushed back one period (closer to the beginning). Deferring payment to a later date means there is an additional period for capitalization. Note that with an annuity the first payment is added up over 3 periods, whereas with a regular annuity it is only added up over 2 periods. Similarly, the second and third payments all have an additional capitalization period in the annuity. Note that it follows from the above formula that both the PV and FV of the annuity due will be higher than the comparable values of conventional annuities.

• Calculate the percentage present value annuity factor (PVIFA) and create a table of PVIFA values.
• Construct a compound interest table for the present value of a regular annuity or the present value of an annuity with payments of $1.

If the pension payments fall at the beginning of the period, they are called pensions due. To calculate the present value rate of an annuity, take the present value rate calculation and multiply it by (1+r), using the discount rate as a variable. The discount rate used to calculate the present value of interest approximates the expected return in future periods.

Understanding the present value of an annuity

The moral is this: Save early and often (and live long!) to take advantage of compound interest. Here we use the same values as in the annuity PV problem above to calculate the PV of the payments at the end of the period (regular annuity) and at the beginning of the period (claimable annuity). Both amortized and regular annuities have a finite number of payments, so it is possible, albeit laborious, to find the PV for each period.

Tables of pensions present value

The first and last payments due on an annuity occur one period earlier than on a regular annuity, so they have a different value in the future. The present value (PV) of an annuity due is the value of today’s series of future payments.

Calculation of present and future value of pensions

These annuities are known as regular annuities (also called deferred annuities). The following table shows a regular 10% annuity over 5 years with equal payments of $5,000 each. Note the similarity to the previous schedule – except that the payment for each year is delayed until the end of the year. This means that each payment will earn less interest for a year and the last payment will earn no interest at all! Note the striking difference between the amount saved on an annuity and a regular annuity ($33,578 versus $30,526).

Balance sheet ratios

Once you have the value of the PVIFA ratio, you can multiply it by the periodic payment amount to find the present value of the annuity. The annuity table above is useful as a quick reference, but it only gives values for individual periods and interest rates that may not exactly match the actual scenario. Therefore, use the annuity formula in the worksheet to more accurately calculate the correct amount of present value annuity due. This task calculates the difference between the present value (PV) of the regular pension and the pension due. The difference in the payment schedule is illustrated in the Excel table.

This is clearly illustrated in the next chapter: Visual comparison of cash flows. This can also be clearly seen in the discount and accumulation graphs drawn in Excel. The present value (PV) of an annuity can be determined by calculating the PV of each individual payment and then adding them together. As with determining the future value (FV) of an annuity, it is important to know when each payment will be made. For amortized annuities, payments are made at the beginning of each period; for periodic annuities, payments are made at the end.What is the present value of $1,000? That’s a question most people don’t think about until they retire and need to save for their golden years. It’s a pretty basic calculation, but it can be a bit daunting to do on your own. A recent post on this blog explored the math behind calculating the present value of annuities, and how you can use it to help choose how much to save for retirement.. Read more about future value of annuity due table and let us know what you think.{“@context”:”https://schema.org”,”@type”:”FAQPage”,”mainEntity”:[{“@type”:”Question”,”name”:”How do you find the present value of an annuity table?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:” The present value of an annuity table is the sum of all the future payments.”}},{“@type”:”Question”,”name”:”How do you find the present value of an annuity of 1?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:” The present value of an annuity of 1 is $1.”}},{“@type”:”Question”,”name”:”How do you find the present value of $1?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:” The present value of $1 is $1.”}}]}

Frequently Asked Questions

How do you find the present value of an annuity table?

The present value of an annuity table is the sum of all the future payments.

How do you find the present value of an annuity of 1?

The present value of an annuity of 1 is $1.

How do you find the present value of $1?

The present value of $1 is $1.